Шухов В. Г. «Определение основных размеров вертикальных цилиндрических резервуаров с плоскими днищами»

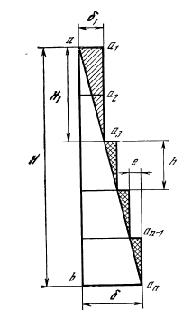
На рисунке изображен схематический разрез резервуара вер­тикальной плоскостью, проходящей через его ось. Обозначения: V — объем резервуара в см2; Н — высота резервуара в см; R — радиус основания резервуара в см; h — а1а2, а2а3, . . ., аn-1аn — высота одного пояса резервуара в см (при общем количестве n поясов); ? — толщина нижнего пояса аn-1аn в см; ?1 — толщина верхних нерасчетных поясов в см; Н1 — часть высоты резервуара с постоянной толщиной стенок в см; е — разность в толщине железа двух последующих поясов в см, ?m — толщина железа в см, эквивалентная весу днища на кв. единицу его основания; ?n — толщина железа в см, эквивалентная весу покрытия на кв. единицу горизонтальной проекции (настил крыши, стропила и пр.); ? — суммарная толщина, равная ?m + ?n, эквивалентная весу днища и покрытия, в см; Т — допускаемое напряжение же­леза в кг/см2; ? — вес одного см3 жидкости, наливаемой в ре­зервуар, в кг/см3; а — коэффициент, равный Т/?, в см; Q — общий объем железа, входящий в состав резервуара, в см3.

При полном наливе резервуара теоретическая толщина его стенок графически выразится прямой ааn (рис. 1) и наибольшее значение этой толщины будет ? = HR?/T = HR/а.

Резервуар должен быть построен таким образом, чтобы нане­сенная графически толщина его поясов везде перекрывала пря­мую ааn. При этом разность в толщине двух последующих поясов изменяется по закону е = Rh?/T = Rh/a.

В зависимости от емкости резервуара расчетная величина ? может быть либо больше, либо меньше ?1; в соответствии с этим при определении наивыгоднейших размеров различаются два рода резервуаров.

Резервуары с переменной толщиной стенок, т. е. резервуары больших емкостей, у которых ?1> ?1.

Резервуары с постоянной толщиной стенок, т. е. резервуары малых емкостей, у которых ?< ?1 (практически ? принимается равным 60. Резервуары с переменной толщи­ной стенок.

Общий объем железа Q, входящий в состав резервуара, может быть разделен на следующие основные части (рисунок):

объем железа дна и крыши q1 = ?R2?;

объем железа, необходимого для сопротивления усилиям, вызываемым налитой жидкостью, или объем напря­женного железа (на рис. 1 соответствует площади ?aanb)

q2 = 2?RH?/2 = nRH?;

объем железа, бесполезного для сопротивления в пределах высоты Н1 (на рис. 1 соответствует заштрихован­ному ?a1aa3),

q3 = ?RH1?1

объем избыточного железа в пре­делах высоты (Н — Н1) соответствует площади треугольников, заштрихованных на рисунке в клетку.

Объем избыточного железа в каждом поясе, где ? > ?1, равен ?Rhe; при общем количестве таких поясов (Н — H1)/h полный объ­ем избыточного железа

g4 = ?Rhe ((H-H1)/h) = ?Re(Н — Н1).

Но так как е = Rh/а, то q4 = ?R2(h/a) (H — Н1).

Таким образом, полный объем железа, идущего на устройство резервуара, будет

Q = q1 + q2 + q3 + q4 = ?R2? + ?RH? + ?RH1?1 + (?R2h/a)H — (?R2h/a)/H1 (A)

Подставляя в это уравнение , ? = RH/a и Н1 = ?1а/R, получим

Q = ?R2? + ?R2H2/a + ??12a + (?R2h/a)H — ?Rh?1

Так как V = ?R2H, то R = ?V/?H. Подставляя это значение R в последнее уравнение для Q, получим

Q = V?/H + VH/a + ??12a + Vh/a — ?1h?(V?/H).

В резервуарах больших емкостей последний член выражения для Q весьма незначителен по сравнению с остальными и без ощу­тительного влияния для результата может быть отброшен.

Выражение для Q принимает вид

Q = V?/H + V(H/a) + ??12a + Vh/a (B)

Для отыскания значения H, при котором Q будет иметь мини­мальное значение, необходимо приравнять первую производную Q по Н нулю

dQ/dH = V (-?/H2 + 1/a) = 0, откуда

H =??a. (1)

Подставляя это значение H в последнее выражение для Q (уравнение В), получим минимальный объем железа, необходи­мый для сооружения резервуара

Qmin = V [2??/a + h/a] ??12a (2)

Из уравнения (1) видно, что при постоянном значении ? и a величина Н остается постоянной; практически это имеет место в резервуарах больших емкостей (свыше 4000 м3), где (по конструк­тивным соображениям) днища имеют толщину 6 мм и вес покры­тия остается почти постоянным на 1 м2 его горизонтальной проек­ции; эти резервуары имеют почти одинаковую высоту (около 11,4 м) и составляются по высоте из восьми поясов.

Уравнение (2) показывает, что один резервуар емкостью V всегда выгоднее по весу, чем равновеликая ему по емкости группа меньших резервуаров: объясняется это тем, что в каждом резер­вуаре, независимо от объема, прибавляется одно и то же количе­ство железа, бесполезного для сопротивления, выражающегося величиной ??12a.

Обращаясь к уравнению dQ/dH = 0, имеем из него равенство

V?/H = VH/a. (3)

Так как по уравнению (В) величина V?/H представляет собой количество железа для дна и покрытия, а VH/a—количество желе­за в стенках, необходимое для восприятия разрывающих усилий, то формула (3) показывает: резервуар с переменной толщиной сте­нок имеет наименьший вес при условии, что объем всего железа дна и покрытия (а следовательно, и его вес) равен объему (а сле­довательно, и весу) всего железа в стенках, необходимого для вос­приятия растягивающих усилий в поясах.

Полученная по формуле (1) теоретическая высота резервуара округляется до размера, кратного ширине стандартных листов (с соблюдением условия минимального количества обрезков при раскрое).

Посмотрим, какое влияние на вес резервуара имеет то или иное отклонение от теоретического значения его высоты. Допустим, что при определении действительной высоты резервуара приходится отступить от теоретической высоты H =??a, заменяя ее высо­той Н’ = ? ??a, где — коэффициент, больше или меньше еди­ницы.

Согласно уравнению (2), объем железа, необходимого для пост­ройки резервуара при высоте последнего Н = ??a

Q = 2V (??/a) + V (h/a)+ ??12a

Подставляя в уравнение (3) значение высоты Н’ = ? ??a, получим объем железа, необходимый для постройки резервуара при этой высоте

Q’ = V (??/a) (? +1/ ?) + V (h/a) + ??12a

Беря отношение

? = Q’/Q = {V (??/a) (? +1/ ?) + V (h/a) + ??12a}{Q = 2V (??/a) + V (h/a)+ ??12a}

и отбрасывая второй и третий члены в числителе и знаменателе дроби, что незначительно отражается на значение ?, получим

? = 1/2(? +1/ ?). (4)

Рассмотрим значение ? на частных примерах: при ? = 0,90 ? =4,0055; ? = 0,95 ? = 1,0013; ? = 1,05 ? = 1,0012; ? = 1,10 ? = 1,0045.

Таким образом, при отклонении высоты резервуара от ее наи­выгоднейшего теоретического значения изменения веса резервуа­ра весьма незначительны; даже при отклонении высоты на 10% в ту или другую сторону вес резервуара увеличивается всего на 0,5% (величина при конструировании почти неуловимая). Послед­нее обстоятельство со всей очевидностью показывает, что переход от теоретического значения высоты Н к ее действительному значе­нию (в соответствии с шириной стандартных листов) практически не отражается на экономичности конструкции.

Резервуары с постоянной толщиной стенок. Подставляя в урав­нение (А) ? = ?1 = const и H = H1 ,получим

Q = ?R2? + 2?RH?1.

Это уравнение может быть написано и непосредственно, так как первый член выражения для Q представляет собой объем желе­за, идущий на дно и покрытие, а второй — объем железа, идущий на стенки.

Подставляя в последнее уравнение R = ?V/?H, получим

Q = V?/H + 2?1 ?V?H. (С)

Приравнивая первую производную Q по Н нулю, получим

dQ/dH = -V(?/H2) + ?1 ?(?V)1/?H

откуда

H = 3 ?(V?2)/(??12) (5)

Подставляя последнее значение Н в уравнение (С), получим минимальный объем железа, необходимого для сооружения резер­вуара

Qmin = 3 3???12?V2 (6)

Подставляя в выражение R = ?V/?H значение Н из уравне­ния (5), получим R = ??1/??, откуда

H/R = ?/?1. (7)

Определяя из последнего уравнения, а также из уравнения ?1= RH/а значения Н и R и подставляя их в выражение объема V = ?R2H, получим предельное значение объема резервуаров, для которых применима формула (5)

V = ??12 3 3?a2/?. (8)

Выше этого значения V для определения высоты резервуара надлежит пользоваться уравнением (1). Из уравнения dQ/dH = 0 имеем

V(?/H2) = ?1??V 1/?V,

или

V ?/H= ?1??VH. (9)

Согласно уравнению (С), величина V?/H представляет собой .количество железа, потребного для дна и покрытия, а ?1??VH — половину количества железа в стенках резервуара; на основании этого можно сделать следующий вывод: резервуар с постоянной толщиной стенок имеет наименьший вес при условии, что объем всего железа дна и покрытия (а следовательно, и его вес) вдвое меньше объема (а следовательно, и веса) всего железа стенок.

Выведем влияние отклонения высоты от ее теоретического зна­чения на вес резервуаров с постоянной толщиной стенок. Соглас­но уравнению (3), объем железа, необходимого для постройки резервуара, при высоте последнего H = 3 ?(V?2)/(??12), составляет

Q = 3?(??12?V2. Допустим, что при определении действительной высоты резервуара приходится отступать от ее теоретического зна­чения, заменяя ее высотой Н’ = ? 3?V?2/??12. Соответствующий этой высоте объем железа, необходимого для постройки резервуа­ра, получим путем замены в уравнении (С) величины Н через Н’.

Q’ = 33 ???12?V2 (1/? + 2??)

Выводя соотношение ? = Q’/Q, получим

? = Q’/Q = 1/3 (1/? + 2??)

Рассмотрим значение е на частных примерах: при ? = 0,90 ? = 1,0033; ? | = 0,95 ? = 1,0006; ? = 1,05 ? = 1,0006; ? = 1,10 ? = 1,0033.

Из значений е видно, что в резервуарах с постоянной толщи­ной стенок отклонения высоты от ее наивыгоднейшего теоретиче­ского значения вызывают еще меньшее изменение веса, чем в ре­зервуарах с переменной толщиной стенок; даже при отклонении высоты на 10% в ту или иную сторону вес резервуара увеличива­ется всего на 0,33 %.